2021 RoboCom 世界机器人开发者大赛-本科组(复赛)
7-1 冒险者分队
冒险者分队是人气 MMORPG《最终幻想 14》里的一个游戏系统。玩家通过招募 NPC (非玩家角色)组成小队完成特定任务后可以获取丰厚的奖励。
由于完成任务有能力的要求,因此我们需要对 NPC 进行一定的训练。NPC 组成的小队会有三个属性:体能、心智,以及战术,玩家可以选择以下的两种训练课程之一对小队进行训练:
- 提升其中一个属性 40,降低其他两个属性各 20;
- 提升其中两个属性 20,降低剩下一个属性 40。
如果在选择的训练课程后有任意一个属性小于 0,那么训练会失败,属性不会发生变化。
为了完成特定任务,现在给定小队的初始属性和目标属性,请回答是否有可能通过一定的训练,使得小队的属性正好达到目标属性的值,如果可以的话,最少的次数是多少?
输入格式:
输入第一行是一个正整数 T (≤105),表示有多少组询问。
接下来的 T 组询问,每组询问有两行,每行三个非负整数,第一行为小队初始的属性,第二行为需要达成的目标属性。
所有属性值均大于等于 0,小于等于 2×109。
输出格式:
如果目标属性无法通过训练达到,输出一行 −1,否则输出一个整数,表示达到目标属性的最少训练次数。
输入样例:
4
25 30 35
65 10 15
100 200 300
200 180 220
100 100 100
0 0 0
777 888 999
777 888 999
输出样例:
1
3
-1
0
解题:数学
思路
首先,初始值与目标值之间只能通过 20 来变换,所以算出每个属性的值变化量并对 20 取模,如果有余数肯定无法转换,把并且由于题目给出的两种训练课程变化量加和都只能为 0 ,所以如果拿到的变化量相加不为 0 的话肯定也不能得到有效答案。以上两种情况直接输出 -1 并返回。
然后,把三个变化量除以 20,简化问题。根据题意得出规律:三个变化量对 3 取模的值必须相同,否则输出 -1 并返回。
最后,考虑构造最优解:设 d1 < d2 < 0 < d3,假设它们分别为 1、1、-2,那么 d2 会首先变成 0,然后,再以两个操作2、-1、-1 和 1、1、-2 组合成 3、0、-3 作用于 d1 和 d3 ,就可以构造出 (0,0,0)(计算公式可以化简)。
代码
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int T;
scanf("%d", &T);
int i1, i2, i3, t1, t2, t3;
while (T--) {
scanf("%d%d%d%d%d%d", &i1, &i2, &i3, &t1, &t2, &t3);
int d1 = i1 - t1, d2 = i2 - t2, d3 = i3 - t3;
if (d1 % 20 || d2 % 20 || d3 % 20 || i1 + i2 + i3 != t1 + t2 + t3) {
printf("-1\n");
continue;
}
d1 /= 20;
d2 /= 20;
d3 /= 20;
if ((d1 % 3 + 3) % 3 != (d2 % 3 + 3) % 3 || (d1 % 3 + 3) % 3 != (d3 % 3 + 3) % 3) {
printf("-1\n");
continue;
}
int weight = (d1 > 0) + (d2 > 0) + (d3 > 0);
if (weight == 0) {
printf("0\n");
continue;
}
if (weight == 2) {
d1 = -d1;
d2 = -d2;
d3 = -d3;
}
int mn = min({d1, d2, d3}), mx = max({d1, d2, d3}), md = d1 + d2 + d3 - mn - mx;
printf("%d\n", (2 * mx + md) / 3);
}
return 0;
}
7-2 拼题A打卡奖励
拼题 A 的教超搞打卡活动,指定了 N 张打卡卷,第 i 张打卡卷需要 mi 分钟做完,完成后可获得 ci 枚奖励的金币。活动规定每张打卡卷最多只能做一次,并且不允许提前交卷。活动总时长为 M 分钟。请你算出最多可以赢得多少枚金币?
输入格式:
输入首先在第一行中给出两个正整数 N(≤103) 和 M(≤365×24×60),分别对应打卡卷的数量和以“分钟”为单位的活动总时长(不超过一年)。随后一行给出 N 张打卡卷要花费的时间 mi(≤600),最后一行给出 N 张打卡卷对应的奖励金币数量 ci(≤30)。上述均为正整数,一行内的数字以空格分隔。
输出格式:
在一行中输出最多可以赢得的金币数量。
输入样例:
5 110
70 10 20 50 60
28 1 6 18 22
输出样例:
40
样例解释:
选择最后两张卷子,可以在 50+60=110 分钟内获得 18+22=40 枚金币。
解题:动态规划 0-1背包问题
思路一(后三个测试点超时)
本题是 0-1背包问题的变形,一般的解法参见:代码随想录 - 0-1背包理论基础。
但是这样做的时间复杂度是 ,根据题目给出的数据范围: ,也就是说最差情况下时间复杂度是 ,肯定会超时。

代码
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N, M;
scanf("%d%d", &N, &M);
vector<int> weights(N), values(N);
for (int i = 0; i < N; ++i) scanf("%d", &weights[i]);
for (int i = 0; i < N; ++i) scanf("%d", &values[i]);
vector<int> dp(M + 1);
for (int i = 0; i < N; ++i) {
for (int j = M; j >= weights[i]; --j) {
dp[j] = max(dp[j], dp[j - weights[i]] + values[i]);
}
}
printf("%d", dp[M]);
return 0;
}
思路二
所以不妨换个思路,观察到题干中数据范围最小的数据是奖励金币数量 ,而打卡卷 也就是物品最大为 ,那么在这个0-1背包问题中最差情况下的最大总价值为 ,所以如果我们在动态规划中先枚举物品,再枚举总价值,最差复杂度仅会达到 是可以过的。动态规划状态转移方程(使用滚动数组):
解释:dp[j] 指总价值为 j 时的最小体积
初始化:
dp[0]:当总价值为 0 时,最小体积一定为 0。- 其他位置 :因为要求的是最小值,所以应该初始化为正无穷(大于最大总价值即可)。
首先在输入数据时顺便维护一个最大总价值(total_value)为所有物品价值的总和(所有打卡卷奖励金币的总和),然后创建一个长度为 total_value + 1 的动规数组,以上面的方式进行动态规划。完成后反向遍历动规数组,找到值小于等于 M 的索引就是最多可以赢得的金币数量。
代码
#include <iostream>
using namespace std;
int main() {
int N, M;
scanf("%d%d", &N, &M);
int weights[N], values[N], c, total_value = 0;
for (int i = 0; i < N; ++i) scanf("%d", &weights[i]);
for (int i = 0; i < N; ++i) {
scanf("%d", &c);
values[i] = c;
total_value += c;
}
int dp[total_value + 1];
fill(dp + 1, dp + total_value + 1, 0x3f3f3f3f);
dp[0] = 0;
for (int i = 0; i < N; ++i) {
for (int j = total_value; j >= values[i]; --j) {
dp[j] = min(dp[j], dp[j - values[i]] + weights[i]);
}
}
while (dp[total_value] > M) total_value--;
printf("%d", total_value);
return 0;
}
7-3 快递装箱

有一条快递装箱的流水线是这样设计的(见下图):

快递件从 A 口进入流水线转盘;到达 B 时进行称重,如果重量大于 W1 就开一个新的箱子把它装进去,否则直接让它通过;到达C时检查箱子的重量,如果超过了 W2(>W1),就直接装车 —— 这条线有 1 号摄像头拍摄装车的箱子编号并记录;重量不达标的箱子或快递件继续行进到 D,在这里进行装箱处理。这里分几种情况:
- 如果 D 当前是空的,那么新开一箱给到达的快递件,或者如果到达的是一只箱子,那么等待下一个快递件到达;
- 如果 D 当前不是空的,那么肯定是有一只箱子。这时考察下一个物体 —— 如果下一个是快递件并且能装入这个箱子(即总重量不超过箱子的最大容量 Wmax ),则将其装入;如果下一个是快递件但装不下了(这时新的快递件装箱),或者下一个来的就是箱子,或者已经没有货物过来了,则停止当前的装箱工作,检查当前这个箱子的重量,超过 W2 就装车 —— 这条线有 2 号摄像头拍摄装车的箱子编号并记录;如果重量不足,则继续前进到 A 口,与新到的快递件汇合。D 点继续处理下一个排队的箱子或快递件。
而到 A 口的箱子则要看汇合的快递件能否装入:如果可以就装箱,向 B 进发;不行就一直等待,直到下一个可以装箱的快递装进去,或者没有任何新的快递到达,才继续向 B 进发。当有多只箱子从 D 转过来时,按到达的顺序排队。
简单起见,我们假设快递件匀速进入流水线,所有快递件从一个点到下一个点都只需要一个单位时间,并且在 B 和 C 的停留时间可忽略不计。当 B 发现重量大于 W1 的是已经在箱子里的货物时,则不必再新开一个箱子。
输入格式:
输入在第一行给出 4 个正整数:N 为快递件的数量;Wmax、W1 和 W2,如题面所述。其中 N≤104,W1<W2<*Wmax*≤103。
随后一行给出 N 个不超过 Wmax 的正整数,为顺序到达的快递件的重量。
输出格式:
在第一行中先后输出第 1、2 号摄像头拍摄的装车箱子的数量、以及最后转盘上剩下的箱子的数量。第二行按非递减序输出剩下的箱子的重量。如果没有箱子剩下,则输出 None。
同一行数字间以 1 个空格分隔,行首尾不得有多余空格。
输入样例:
11 100 50 80
85 25 60 21 10 52 80 95 78 15 3
输出样例:
2 1 4
40 55 78 80
样例说明:
我们按照“单位时间:事件”的格式描述整个过程。
| 时间 | A | B | C | D |
|---|---|---|---|---|
| 1 | 85 | - | - | - |
| 2 | 25 | 85装箱 | - | - |
| 3 | 60 | 25 | 85装车,1号拍摄 | - |
| 4 | 21 | 60装箱 | 25 | - |
| 5 | 10 | 21 | 60一箱 | 25装箱 |
| 6 | 52 | 10 | 21 | 60一箱到,25一箱启动 |
| 7 | 80不能装箱,25一箱等待 | 52装箱 | 10 | 21装箱得到81一箱 |
| 8 | 95不能装箱,25一箱等待 | 80装箱 | 52一箱 | 10装箱得到91一箱 |
| 9 | 78不能装箱,25一箱等待 | 95装箱 | 80一箱 | 52一箱到,91一箱装车,2号拍摄 |
| 10 | 15装箱得到40一箱 | 78装箱 | 95一箱装车,1号拍摄 | 80一箱到,52一箱启动 |
| 11 | 3装箱得到55一箱 | 40一箱 | 78一箱 | 80一箱 |
此时摄像头 1 拍摄了 2 次,摄像头 2 拍摄了 1 次,转盘上还剩 4 只重量为 55、40、78 和 80 的箱子。
解题:待补充
7-4 塔防游戏

有一种简单的塔防游戏是这样的:给定一张由 n 行 m 列个方格子构成的地图,玩家可以任选一个格子放置自己的大本营,还可以在任意一个格子里放置自己的防御堡垒。大本营和每个防御堡垒都有自己的防御能力值 d,表示可以抵御 d 个僵尸的攻击。每一轮游戏开始时,玩家在规定时间内将本级别可以用的防御堡垒布置在地图中,然后僵尸们就从地图边界涌入地图中,向着大本营发起攻击。每轮进攻持续一个固定的时长,结束后剩余的僵尸就原地蒸发。
每队僵尸可以向一个方格的上下左右四个方向移动。如果相邻的目标方格没有堡垒,它们就可以用 1 秒的时间移动过去,否则会被堡垒阻挡或者消灭。对每一队僵尸(从同一地点出发的所有僵尸)而言,每秒会被堡垒消灭 1 个队友,同时消耗掉该堡垒 1 个单位的防御能力。当防御能力降为 0,则该堡垒消失,剩下的僵尸则用 1 秒移动到这个方格继续行进。注意:如果有多支僵尸队都进入了同一个方格,它们并不会合并成一支队伍。
所有的僵尸队都会根据进攻开始时的地图选择被歼灭最少的到达大本营的路线,并且一直按照这个路线行进,中途不因为地图状态的改变而改变。当这样的进攻路径不唯一时,选择能最快到达大本营的路径。题目保证这样的路径所打掉的堡垒的布局是唯一的。
本题就要求你计算出一轮攻击结束时,地图上的布局情况。
输入格式:
输入首先在第一行中给出三个正整数:不超过 100 的 n 和 m,为地图的尺寸;不超过 1000 的 T,为一轮攻击持续的时长。
随后给出 n+2 行,每行给出 m+2 个数字,每行中的数字都用空格分隔,表示攻击开始前地图上的布局。其中第 1 行、第 1 列、第 n+2 行、第 m+2 列是地图边界外僵尸们出发的位置,这些位置上,0 表示没有僵尸,其他正整数表示从该位置出发的僵尸们的数量。而地图中的每个位置上,0 表示没有堡垒,其它正整数表示该位置上堡垒的防御能力值。大本营是一个特殊的建筑,我们用一个负数 −D 表示这里是大本营,其防御能力值为 D。这里的防御值和任一队僵尸的数量都不超过 100。
注意:僵尸不可在地图边界外移动,它们的第一个移动目标必须在地图中,所以四个角落里出现的僵尸可以被忽略,因为它们没有进入地图的途径。
输出格式:
输出 n 行,每行 m 个数字,对应攻击结束后地图上每个方格的状态。状态的表示与输入相同:没有堡垒的地方输出 0,有堡垒的地方输出其剩余防御值,大本营的位置上输出其剩余防御值的负值。
注意每行数字间以 1 个空格分隔,行首尾不得有多余空格。
当大本营被攻陷时,游戏即刻结束。此时应输出结束时的地图状态,并且在最后一行输出一句 Game Over。
输入样例 1:
7 5 17
0 0 0 0 13 0 0
0 0 0 0 0 0 0
0 0 0 8 0 0 0
0 0 0 0 2 1 0
0 0 0 7 5 3 0
8 0 1 4 -10 1 0
0 0 0 3 3 0 0
0 0 8 0 9 0 0
0 0 0 4 0 0 0
输出样例 1:
0 0 0 0 0
0 0 8 0 0
0 0 0 2 0
0 0 7 5 0
0 0 0 -1 0
0 0 0 2 0
0 8 0 9 0
样例说明:
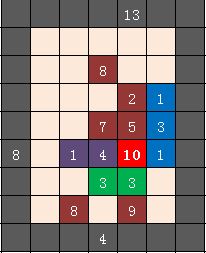
地图布局如下图所示。
规模为 13 和 8 的两队僵尸都有两种选择,攻打蓝色或者紫色堡垒都是消耗最少的。在这种情况下,规模为 13 的僵尸队走蓝色比较快,需要 1+1+1+2+4+2=11 秒到达大本营边上;规模为 8 的僵尸队走紫色比较快,需要 1+2+5=8 秒到达大本营边上。
规模为 4 的僵尸队比较惨,只能选择绿色堡垒,最后被大本营边上的绿色堡垒消灭。注意到在攻击过程中,其实它们可以等到紫色堡垒被攻陷之后走紫色原始值为 4 的方格,但是因为路径是在初始状态下选定就不能改的,所以它们不能这样选择。
攻打大本营时,规模为 8 的僵尸队剩下了 3 只先到达,在第 11 秒被大本营消灭。此时大本营还剩 7 个单位的防御值,同时规模为 13 的僵尸队剩下的 8 只进入了大本营相邻的方格,开始攻击。但此时距离本轮结束只剩 6 秒,结果大本营在结束时还剩 1 个单位的防御值,玩家胜。
输入样例 2:
7 5 20
0 0 0 0 13 0 0
0 0 0 0 0 0 0
0 0 0 8 0 0 0
0 0 0 0 2 1 0
0 0 0 7 5 3 0
8 0 1 4 -10 1 0
0 0 0 3 3 0 0
0 0 8 0 9 0 0
0 0 0 4 0 0 0
输出样例 2:
0 0 0 0 0
0 0 8 0 0
0 0 0 2 0
0 0 7 5 0
0 0 0 0 0
0 0 0 2 0
0 8 0 9 0
Game Over
样例说明:
样例 2 与样例 1 唯一的区别在于攻击时长变为 20。但实际上,攻击在第 18 秒就结束了。




评论区